Модель извлечения фактов из естественно-языковых текстов и метод ее обучения
Андреев А.М., Березкин Д.В., Симаков К.В.
НПЦ "ИНТЕЛТЕК ПЛЮС"
arka@inteltec.ru
Аннотация
В статье изложена модель извлечения фактов из естественно-языковых текстов и метод ее обучения. Ключевым элементом
модели является набор правил извлечения. Метод обучения генерирует набор правил на основе обучающих примеров подготовленных человеком.
Проведен ряд экспериментов, дана оценка зависимости основных показателей качества обученной модели от свойств исходной обучающей выборки.
Введение
Данная работа посвящена извлечению фактов из естественно-языковых текстов для системы выявления несоответствий и
противоречий в документах определенной предметной области. Концепция создания такой системы изложена в [14] и получила своё развитие
в ряде исследований, одно из которых рассмотрено в данной работе. Задача извлечения также актуальна в связи с активным развитием технологий
Semantic Web. Данные технологии делают основной упор на представлении и манипулировании знаниями, оставляя без внимания вопрос приобретения
знаний, большое количество которых накоплено в неструктурированных естественно-языковых текстах. Предлагаемый в данной работе подход к
извлечению может быть использован для решения отмеченной проблемы.
Постановка задачи
В данной работе используется представление фактов в виде фреймов [12].
Фрейм рассматривается как структура, с поименованными элементами - слотами. Фреймы и слоты наделяются определенной семантикой, в зависимости
от предметной области, в которой они используются. Например, фрейм может описывать событие некоторого типа, тогда слоты интерпретируются
как роли участников данного события. Задача извлечения сводится к выявлению в анализируемом тексте факта присутствия некоторого фрейма
fi и означиванию его слотов {sj} фрагментами из данного текста.
Выполним более строгую постановку задачи. Пусть знания о предметной области представлены множеством фреймов F. Каждый фрейм
fi  F имеет набор слотов {sj}. Анализируемый текст t представлен последовательностью элементарных
текстовых элементов {wi}, которыми могут быть слова и знаки препинания. Задача извлечения заключается в формировании
для анализируемого текста набора троек вида <fi,sj,tk>, где fi - фрейм из
предопределенного множества F, sj - слот данного фрейма, tk - фрагмент анализируемого текста t,
являющийся выявленным в тексте t значением слота sj. F имеет набор слотов {sj}. Анализируемый текст t представлен последовательностью элементарных
текстовых элементов {wi}, которыми могут быть слова и знаки препинания. Задача извлечения заключается в формировании
для анализируемого текста набора троек вида <fi,sj,tk>, где fi - фрейм из
предопределенного множества F, sj - слот данного фрейма, tk - фрагмент анализируемого текста t,
являющийся выявленным в тексте t значением слота sj.
Основные методы извлечения
Методы извлечения на основе признаков (feature-based) подразумевают наличие фиксированного набора признаков (feature dictionary)
и весов использования этих признаков в окрестности извлекаемых элементов текста. Для каждого извлекаемого элемента определяется характеризующий
его вектор признаков. Наиболее распространенными в данном классе являются вероятностные классификаторы Байеса и [1] и
Скрытые Марковские Модели (Hidden Markov Models)[2]. Извлечение сводится к распознаванию некоторого сегмента текста на
основе вероятностного анализа признаков, обнаруженных в окрестности этого сегмента. Недостатками таких подходов является использование
ограниченного размера окрестности (как правило, не боле 2-3 слов), необходимое для обеспечения требуемой точности извлечения. Использование
большего размера контекста приводит к снижению полноты распознавания и к увеличению размера необходимой репрезентативной выборки, на
которой собирается статистика для расчета оценок вероятностей.
Методы извлечения, использующие ядра (kernel-based) [3], решают часть недостатков
предыдущего класса за счет алгоритмического определения меры подобия между представлениями сопоставляемых текстовых сегментов. Суть
методов - заменить скалярное произведение векторов, отражающих признаковое представление распознаваемых элементов, некоторой функцией - ядром.
Такая функция зада-ется алгоритмически и учитывает более сложное представление распознаваемых элементов и их контекстов, как правило
древовидное, описывающее синтаксическую структуру текстового сегмента. Для древовидных представлений расчет ядра чаще всего сводится к
сопоставлению всех вложенных деревьев в исходные. Недостатком такого подхода является высокая вычислительная сложность расчета ядер и
определения синтаксической структуры текстового сегмента.
Методы, основанные на сопоставлении образцов (pattern-based) [4], [5],
оперируют понятием "образец" и правилами их сопоставления с фрагментами текстов. Образцы представляют собой цепочки ограничителей
(символы, слова, части речи и семантические классы). Такие цепочки являются своего рода шаблонами фраз. В этом отношении данный метод
аналогичен ядерному подходу при условии, что текстовые сегменты имеют "плоское" представление, а не древовидное. Особенность заключается
в методе обучения, в основе которого лежат приемы индуктивного логического программирования (Inductive Logic Programming).
Методы, основанные на фразовых образцах (phrase-based), являются своего рода компромиссом между kernel-based
и pattern-based методами. Текстовые сегменты также как и в kernel-based подходах представляются деревьями синтаксического разбора [6],
но вместо сложного расчета ядер выполняется более простая с точки зрения вычислительной сложности процедура сопоставления с синтаксическим
шаблоном [7], присущая pattern-based методам, но в дополнении к морфологическим признакам использующая при сопоставлении
синтаксические связи [8]. Чаще всего, для отражения синтаксических связей используется контекстно-свободная грамматика или
одна из ее модификаций, например Стохастическая Контекстно-Свободная Грамматика [9]. Применение таких грамматик позволяет
оценить вероятность применения того или иного правила для рассматриваемого участка текста и выбрать правило, вероятность применения
которого максимальна. Получение грамматики заключается в ручном составлении формальных правил и вычислении оценок вероятностей их
употребления на некоторой обучающей выборке текстов, предварительно размеченной человеком. В дополнении к выделенным элементам извлечения
разметка содержит указания на правила грамматики, которые необходимо применять при извлечении данных элементов.
Описываемый в данной работе метод относится к pattern-based методам, адаптированным к применению для
русского языка. Отличительными особенностями подхода являются:
- работоспособность при условии неоднозначности морфологического разбора отдельных слов,
- работоспособность метода обучения в условиях "зашумленности" обучающих примеров, т.е. примеров, содержащих как ошибки эксперта-составителя,
так и естественно-языковые исключения,
- высокая производительность метода, достигаемая за счет использования методов оптимального поиска,
- комбинированный характер использования обучающих примеров - одновременное использование сжимающей и покрывающей парадигм использования
входной обучающей выборки.
Модель извлечения
В качестве основы взята pattern-based модель, основанная на образцах. Образцы по аналогии с [4]
представляют собой шаблоны фраз, состоящие из элементов, связанных отношением предшествования [5]. Иными словами, в рамках
образца элементы представляют собой последовательность вида
p=r1r2···rn (1)
где ri - i-ый элемент образца. Для любой пары эле-ментов образца (ri; rj) элемент ri
предшествует эле-менту rj, если i < j. Роль образца как шаблона фразы заключается в том, что при извлечении
информации из некоторого текста на основе данного образца элементы текста должны следовать друг за другом в том же порядке, в каком следуют
друг за другом соответствующие им элементы образца. Т.е. для каждого элемента анализируемого текста должен присутствовать соответствующий
ему элемент образца. Тексты, одинаковые по содержанию, но различные по форме написания относятся к разным образцам.
Минимальными элементами текста являются слова и знаки препинания. Более крупные текстовые элементы
не рассматриваются, более того анализ текста выходит за рамки отдельных предложений. Т.е. границы предложений не рассматриваются как границы
анализируемых контекстов текста. Выполняется сквозной анализ, игнорируя границы предложений. Вместе с тем символы, обозначающие границы предложений,
рассматриваются как полноценные текстовые элементы наравне со словами и другими знаками препинания. Удобно ввести понятие текстового сегмента,
который представляет собой некоторую последовательность минимальных текстовых элементов вида
t=w1w2···wm (2)
Где t - некоторый текстовый сегмент, подлежащий анализу, wi - i-ый текстовый элемент (слово или знак препинания) сегмента.
В таком определении, текстовым сегментом может быть как последовательность слов предложения, так и последовательность слов из нескольких соседних
предложений текста. Под длиной | t | сегмента будем подразумевать количество текстовых элементов, составляющих сегмент t.
Под сцеплением сегментов и будем подразумевать сегмент такой, что элементы с номерами 1...| t1 | сегмента t
совпадают с элементами сегмента t1, а элементы с номерами |t1|...|t| совпадают
с элементами сегмента t2. Для отражения факта сцепления будем использовать запись
t=t1 + t2 +...+tn (3)
В модели извлечения ключевую роль играют элементы образцов. Каждый элемент ri некоторого
образца задает множество Tri={t} текстовых сегментов. Все элементы всех образцов задают предельно допустимую сегментацию
текстов, так что с точки зрения модели извлечения в тексте можно выделить только сегменты из Tr и сегменты, полученные в
результате их сцепления. Элемент образца представляет собой четверку вида
ri=<c,e,l1,l2> (4)
Где c - лексическое ограничение, e - исключение лексического ограничения, l1 и l2 - минимальная
и максимальная длина покрытия элемента. Лексическое ограничение c и его исключение e определяют множество текстовых
элементов c\e={w}, которые могут встречаться в текстовых сегментах Tri={t}, задаваемых элементом ri.
Множество c определяет допустимые текстовые элементы в сегментах Tri, тогда как множество e задает исключения из c, т.е.
текстовые элементы, употребление которых запрещено в сегментах Tri. Минимальная и максимальная длины покрытия l1 и
l2 определяют допустимый диапазон длин текстовых сегментов Tri. Например, значения l1=0 и l1=2
означают, что Tri состоит из текстовых сегментов таких, что
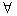 t t  Tri → 0≤ | t | ≤ 2. Таким образом множество текстовых сегментов Tri
задается элементом ri=<c,e,l1,l2> следующим образом Tri → 0≤ | t | ≤ 2. Таким образом множество текстовых сегментов Tri
задается элементом ri=<c,e,l1,l2> следующим образом
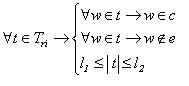 (5) (5)
Далее для определенности будем говорить, что элемент ri покрывает некоторый сегмент t,
если t  Tri, этот факт будем отражать логической функцией a(t,ri),
принимающей значение "истина", если выполнены условия (5), в противном случае a(t,ri)="ложь". Из определения минимальной
длины покрытия элемента следует, что любой элемент с l1=0 покрывает пустой сегмент, т.е. сегмент, не содержащий ни одного
текстового элемента. Tri, этот факт будем отражать логической функцией a(t,ri),
принимающей значение "истина", если выполнены условия (5), в противном случае a(t,ri)="ложь". Из определения минимальной
длины покрытия элемента следует, что любой элемент с l1=0 покрывает пустой сегмент, т.е. сегмент, не содержащий ни одного
текстового элемента.
С учетом введенной модели сегмента текста и элемента образца более точно роль образца, как последовательности
элементов вида (4), можно определить следующим образом. Образец p=r1r2···rn описывает некоторое множество текстовых сегментов Tp={t} так, что
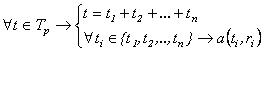 (6) (6)
Иными словами, образец p задает множество сегментов Tp таких, что каждый сегмент
t  Tp может быть представлен в виде сцепления некоторых сегментов t1,t2,...,tn,
каждый из которых покрывается элементом r1,r2,...,rn образца соответственно. Выражение (6) предоставляет
метод проверки для произвольного сегмента t факта его принадлежности к Tp от некоторого образца p.
Таким образом, если для сегмента t удается подобрать сегменты t1,t2,...,tn, удовлетворяющие (6),
то можно делать вывод о том, что t Tp может быть представлен в виде сцепления некоторых сегментов t1,t2,...,tn,
каждый из которых покрывается элементом r1,r2,...,rn образца соответственно. Выражение (6) предоставляет
метод проверки для произвольного сегмента t факта его принадлежности к Tp от некоторого образца p.
Таким образом, если для сегмента t удается подобрать сегменты t1,t2,...,tn, удовлетворяющие (6),
то можно делать вывод о том, что t  Tp. В этом случае будем говорить, что образец p
покрывает сегмент t, этот факт будем отражать логической функцией a(t,p), принимающей значения "истина" или "ложь"
в зависимости от того, выполнены условия (6) или нет. Tp. В этом случае будем говорить, что образец p
покрывает сегмент t, этот факт будем отражать логической функцией a(t,p), принимающей значения "истина" или "ложь"
в зависимости от того, выполнены условия (6) или нет.
Лексические ограничения элементов образцов и их исключения можно задавать разными способами (см. рис. 1),
начиная от поэлементного перечисления слов и заканчивая предопределенными классами (например, класс слов с общими морфологическими признаками).
Особенное внимание необходимо уделить семантическим классам. Такая классификация слов может быть доступна во внешних источниках, таких как
толковые словари [15] или тезаурусы. Например, во многих словарях в толкованиях слов можно встретить метки, относящие слова к той или иной сфере
применения (медицина, юриспруденция, техника и др.)[16], которые можно использовать для более точного задания лексических ограничений.
Другим примером источника семантических классов является русскоязычный тезаурус типа WordNet [13], в этом случае в качестве семантических классов
можно напрямую использовать синсеты данного тезауруса.
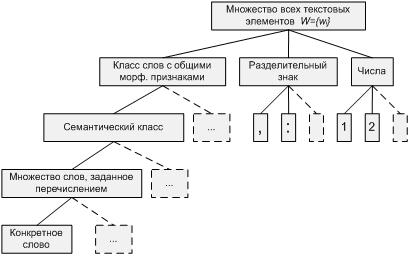
Рис. 1. Группы слов, задаваемых ограничениями.
По аналогии с [4] для извлечения информации из текста используются правила. Отличие заключается в том, что в
нашем случае элементы образцов имеют представление вида 4, т.е. могут учитывать запрещенные текстовые элементы, позволяют задавать наборы
морфологических признаков (вместо одной части речи), а также позволяют указывать диапазоны (l1,l2) в рамках которых
распространяется действие лексического ограничения. Правила извлечения представляют собой тройки вида
v=(pb , pc , pa) (7)
Где pb - префиксный образец, pc - образец, извлекающий информацию из текста (в данном случае понятие),
pa - постфиксный образец. Первый и последний образцы описывают контекст употребления извлекаемого сегмента слева и справа
соответственно. Извлекающий образец описывает непосредственно структуру текстового сегмента, подлежащего извлечению, в процессе означивания
определенного слота некоторого фрейма. По сути, правило v=(pb , pc , pa) задает множество текстовых сегментов Tv={t}, таких что
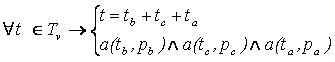 (8) (8)
Т.е. правило v задает множество текстовых сегментов Tv таких, что каждый сегмент t  Tv
может быть представлен в виде сцепления трех сегментов tb , tc , ta каждый из которых покрывается
соответственно образцом pb , pc , pa составляющим правило v. Tv
может быть представлен в виде сцепления трех сегментов tb , tc , ta каждый из которых покрывается
соответственно образцом pb , pc , pa составляющим правило v.
Обобщенно модель извлечения можно описать алгебраической системой вида
E=<T , V , a> (9)
Где T - множество всех анализируемых текстовых сегментов, V - множество правил извлечения вида (7), a - логическая функция,
позволяющая для любого текстового сегмента t  T и любого правила v T и любого правила v  V
сделать вывод о принадлежности сегмента t множеству Tv. Выражение (8) предоставляет метод для такой проверки.
Так, если для сегмента t удается подобрать сегменты tb , tc , ta, удовлетворяющие (8),
то можно делать вывод о том, что t V
сделать вывод о принадлежности сегмента t множеству Tv. Выражение (8) предоставляет метод для такой проверки.
Так, если для сегмента t удается подобрать сегменты tb , tc , ta, удовлетворяющие (8),
то можно делать вывод о том, что t  Tv. В этом случае будем говорить, что правило v
покрывает некоторый сегмент t, при этом функция a(t,v) принимает значение "истина", в противном случае функция a(t,v)
принимает значение "ложь". Кроме установления факта покрытия a(t,v), выражение (8) выявляет сегмент tc,
подлежащий извлечению. Tv. В этом случае будем говорить, что правило v
покрывает некоторый сегмент t, при этом функция a(t,v) принимает значение "истина", в противном случае функция a(t,v)
принимает значение "ложь". Кроме установления факта покрытия a(t,v), выражение (8) выявляет сегмент tc,
подлежащий извлечению.
Метод извлечения
Имея модель (9), метод извлечения сводится к поиску для некоторого сегмента текста
t  T подмножества подходящих правил v. Основной проблемой данного подхода
является вычислительная сложность, связанная с перебором имеющихся правил v T подмножества подходящих правил v. Основной проблемой данного подхода
является вычислительная сложность, связанная с перебором имеющихся правил v  V и установлением
факта покрытия a(t,v). Проблема усугубляется тем, что один и тот же сегмент t может быть покрыт несколькими правилами.
Хотя проблема неоднозначного толкования решается на этапе сборки всего фрейма, когда имеется полная информация о вариантах означивания
каждого слота, желательно сократить число генерируемых вариантов означивания конкретного слота уже на текущем этапе. V и установлением
факта покрытия a(t,v). Проблема усугубляется тем, что один и тот же сегмент t может быть покрыт несколькими правилами.
Хотя проблема неоднозначного толкования решается на этапе сборки всего фрейма, когда имеется полная информация о вариантах означивания
каждого слота, желательно сократить число генерируемых вариантов означивания конкретного слота уже на текущем этапе.
Представление правила (7) удобно при рассмотрении метода обучения. Для решения же задачи выбора
оптимального правила удобней рассматривать правило как образец вида (1). Такой образец формируется из элементов образцов pb , pc и pa,
так что последний элемент образца pb предшествует первому элементу образца pc, а последний
элемент образца pc предшествует первому элементу образца pa.
Задача метода извлечения - выполнить оптимальный поиск K подходящих правил из множества
V модели E для означивания слота текстовым сегментом t. Для выполнения оптимального поиска удобно использовать
метод ветвей и границ. Для получения отсекающего критерия введем следующее предположение. Будем считать, что при анализе сегмента t
правило v1 является предпочтительней по отношению к правилу v2, если степень конкретности правила
v1 больше степени конкретности правила v2 применительно к этому сегменту. Степень конкретности
правила определим как
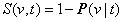 (10) (10)
где P(v|t)- вероятность использовать где-либо правило v, при условии, если достоверно известно, что оно покрывает сегмент t.
Таким образом, чем больше условная вероятность применения правила, тем менее оно конкретно. Вероятность P(v|t) определяется следующим
образом. Пусть правило v=r1...rn покрывает сегмент t так, что сегмент может быть представлен в виде
сцепления t=t1+t2+...+tn, каждый сегмент ti которого покрывается соответствующим
элементом ri правила. Заменим в каждом элементе ri длины покрытий l1 и l2
так, чтобы 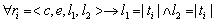 , получив тем самым модифицированное правило v'. Такая замена гарантирует, что v' будет
покрывать только текстовые сегменты, представимые в форме t=t1+t2+...+tn. Таким образом, условную
вероятность P(v|t) можно заменить безусловной P(v'), которая рассчитывается согласно (11) , получив тем самым модифицированное правило v'. Такая замена гарантирует, что v' будет
покрывать только текстовые сегменты, представимые в форме t=t1+t2+...+tn. Таким образом, условную
вероятность P(v|t) можно заменить безусловной P(v'), которая рассчитывается согласно (11)
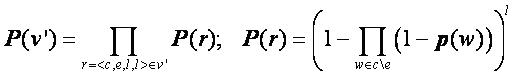 (11) (11)
где p(w) - вероятность встретить в тексте текстовый элемент w. Оценка (11) вероятности P(v|t) не является точной,
поскольку не учитывает порядок следования элементов внутри правила. Учет порядка следования существенно усложнит модель (11), что приведет
к противоположному результату - увеличению вычислительной сложности алгоритма извлечения. С учетом сказанного алгоритм поиска K оптимальных
правил, покрывающих сегмент t сводится к следующему.
w1...wm - анализируемый сегмент текста
Q - очередь длины K, сохраняющая наиболее предпочтительные правила
V = множество всех правил модели извлечения E
min = 0
Цикл для i =1...m
t=w1...wm наращиваем анализируемую последовательность
Vc = {v V}: S(v,t)> min
Vi = {v Vc}: a(t,v)=true
Пропустить все правила из Vi через очередь Q
min = предпочтительность последнего правила очереди Q
i = i + 1
V = V \ Vi
Конец цикла
Рис. 2. Алгоритм оптимального поиска правил.
Входной информацией для алгоритма является анализируемый сегмент текста w1...wm.
Результат анализа сохраняется в очереди Q, имеющей ограниченную предельную длину K. В очереди Q правила отсортированы по
убыванию предпочтительности, так что последним правилом в очереди является правило с минимальной предпочтительностью. Изначально очередь
Q пуста. Алгоритм анализирует входной сегмент последовательно, начиная с последовательности из одного текстового элемента и
прибавляя к ней на каждом шаге по одному элементу. На каждом шаге из множества всех правил V выбираются правила Vc,
не подпадающие под действие отсекающего критерия, а затем из них отбираются правила Vi, соответствующие текущей
последовательности текстовых элементов t. Отобранные правила пропускаются через очередь Q, где они размещаются в соответствии
с рассчитанной предпочтительностью. При этом правила с предпочтительностью меньшей, чем у последнего K-ого элемента очереди,
отбрасываются и далее не рассматриваются. По окончании шага исходное множество правил V сокращается - из него удаляются правила
Vi, выделенные на данном шаге.
Ключевым шагом алгоритма является проверка отсекающего критерия перед выявлением соответствия a(t,v).
До тех пор, пока алгоритм не найдет хотя бы одно правило, соответствующее входной последовательности, на каждом шаге будет выполняться полный
поиск правил с вычислением a(t,v) для всего множества V. Однако, как только будет получено первое непустое множество Vi
и будет вычислено значение min, отличное от нуля, исходная область дальнейшего поиска (множество V) будет сокращаться до
множества правил Vc, успешно прошедших отсекающий критерий S(v,t) > min.
Метод обучения модели извлечения
Задача обучения заключается в генерации множества правил V модели извлечения E. Разработанный метод обучения относится к методам,
основанным на примерах (example-based), идея которых заключается в генерации правил извлечения на основе обучающих примеров, подготовленных
человеком-экспертом. Главными преимуществами такого подхода, по сравнению с непосредственным написанием правил экспертом, является
меньшая квалификация человека, необходимая для подготовки обучаемых примеров, и меньшие трудозатраты на составление правил.
Представление обучающих примеров
В существующих подходах [4, 11, 8, 9, 7] принято использовать позитивные примеры обучения, т.е. примеры, являющиеся подтверждающим свидетельством
применения генерируемого правила. В отличие от указанных работ, представление элементов образцов в нашем случае позволяет использовать
исключения (см. 4), для получения правил с такими элементами необходимо использовать негативные примеры, т.е. примеры, являющиеся опровергающим
свидетельством применения генерируемого правила.
Дадим формальное определение обучающего примера. Предположим, что у нас имеется некоторое множество
уникальных маркеров M, которыми мы можем пометить все извлекаемые элементы, в нашем случае такими элементами являются пары вида
< fi,sj> = < фрейм, слот в рамках фрейма >. Обучающим примером является текстовый сегмент вида 12,
наделенный маркерами из множества M. Задача маркеров - установить однозначное соответствие между текстовыми элементами сегмента
и извлекаемыми элементами модели предметной области (фреймы и слоты)
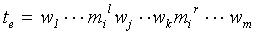 (12) (12)
где w1...wm - текстовые элементы сегмента, wj...wk - выделенный маркером
mi  M фрагмент, mil - элемент, обозначающий левую
границу выделенного фрагмента маркером mi, mir - элемент, обозначающий правую границу
выделенного фрагмента. Метод обучения использует обучающую выборку Te={te} примеров вида 12. Задача
обучения - получить на основе Te множество правил V модели извлечения E. Поскольку модель извлечения
предполагает, что маркеры встречаются независимо друг от друга, то обучающую выборку Te можно представить
как Te=Tm1 M фрагмент, mil - элемент, обозначающий левую
границу выделенного фрагмента маркером mi, mir - элемент, обозначающий правую границу
выделенного фрагмента. Метод обучения использует обучающую выборку Te={te} примеров вида 12. Задача
обучения - получить на основе Te множество правил V модели извлечения E. Поскольку модель извлечения
предполагает, что маркеры встречаются независимо друг от друга, то обучающую выборку Te можно представить
как Te=Tm1 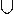 Tm2 Tm2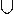 ... ...
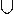 Tm, где Tmi - непересекающиеся подмножества обучающих примеров,
каждое такое подмножество содержит примеры только для одного маркера mi из M. Опираясь на такое представление
можно выполнять обучение для каждого из подмножеств независимо. По аналогии с [5] и [4] в качестве
позитивных примеров обучения, отмеченных маркером mi, будем считать примеры из обучающей выборки Tmi. В качестве
негативных примеров, отмеченных маркером mi, будем считать любой текстовый сегмент, не входящий в Tmi,
т.е. множество T \ Tmi, где T - множество все допустимых текстовых сегментов. Tm, где Tmi - непересекающиеся подмножества обучающих примеров,
каждое такое подмножество содержит примеры только для одного маркера mi из M. Опираясь на такое представление
можно выполнять обучение для каждого из подмножеств независимо. По аналогии с [5] и [4] в качестве
позитивных примеров обучения, отмеченных маркером mi, будем считать примеры из обучающей выборки Tmi. В качестве
негативных примеров, отмеченных маркером mi, будем считать любой текстовый сегмент, не входящий в Tmi,
т.е. множество T \ Tmi, где T - множество все допустимых текстовых сегментов.
Описание метода
По направлению процесса обучения методы данного класса разделяются на методы, действующие "снизу-вверх", и методы, действующие "сверху-вниз".
Первые выполняют последовательное обобщение правил, итеративно генерируя из конкретных правил правила более общие. Методы "сверху-вниз" двигаются
в обратном направлении: от общих правил к правилам более конкретным. В обоих случаях критерием генерации правила является максимальное количество
покрываемых правилом позитивных примеров и минимальное количество покрываемых правилом негативных примеров. По способу использования обучающих
примеров методы разделяются на "сжимающие" и "покрывающие". Сжимающие методы на каждой итерации используют все примеры обучающей выборки
Te, в то время как покрывающие методы отбрасывают из дальнейшего рассмотрения обучающие примеры, на основе которых сгенерировано
правило. В данной работе применяется подход "снизу-вверх", по способу использования обучающих примеров разработанный метод является сжимающим с
некоторыми особенностями. Обучение в данной работе можно рассматривать как итеративный поиск максимума функции качества модели извлечения
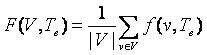 (13) (13)
Где |V| - количество правил извлечения множества V, f(v,Te) - функция качества отдельно взятого правила v.
В ходе обучения на каждой итерации состав множества V изменяется так, чтобы максимизировать функцию F(v,Te).
Если считать, что обучающая выборка Te является репрезентативной для заданной предметной области, то можно считать,
что полученный в ходе оптимизации набор правил V применим и для любого набора текстов предметной области. Для оценки качества
отдельного правила f(v,Te) в данной работе используется объединенный показатель точности и полноты (14), используемый в
аналогичных работах [2]
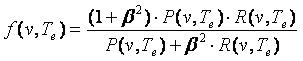 (14) (14)
Где P(v,Te) - точность извлечения правила v, R(v,Te) - полнота извлечения правила, β - вес,
определяющие значимость полноты по отношению к точности, в данной работе использовался β =1. Поскольку
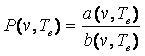 и и 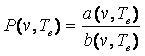
где a(v,Te) - количество корректно извлеченных сегментов правилом v, b(v,Te) - общее количество извлеченных
сегментов правилом v, d(v,Te) - требуемое количество извлеченных сегментов, которые должно покрыть в идеале правило v.
Поскольку в идеале каждое правило должно стремиться покрыть всю обучающую выборку, примем d(v,Te)=|V|. С учетом сказанного
функция качества f(v,Te) отдельного правила примет вид (15)
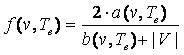 (15) (15)
Тогда функция качества модели извлечения F(V,Te) запишется как
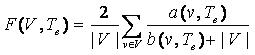 (16) (16)
Поиск глобального максимума функции (16) представляет собой NP сложную задачу, поэтому в данной работе представлен метод, определяющий локальный
максимум этой функции с вычислительной сложностью 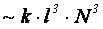 , где l - средняя длина обучающего примера,
N - количество обучающих примеров. Разработанный метод можно разделить на следующие этапы: формирование предельно конкретных правил,
итеративное обобщение, деградация, генерация исключений. Рассмотрим основные этапы метода обучения подробнее. , где l - средняя длина обучающего примера,
N - количество обучающих примеров. Разработанный метод можно разделить на следующие этапы: формирование предельно конкретных правил,
итеративное обобщение, деградация, генерация исключений. Рассмотрим основные этапы метода обучения подробнее.
Формирование предельно конкретных правил
Формирование предельно конкретных правил выполняется на основе позитивных примеров вида (12), каждый такой пример объявляется правилом вида (7).
Префиксный образец pb формируется на основе последовательности текстовых элементов примера te, предшествующих
элементу разметки ml. Образец формируется из элементов ri=<c,e,l1,l2> так, что
лексическое ограничение c представляет собой множество из одного текстового элемента wi примера te,
исключение e лексического ограничения представляет собой пустое множество, а количества повторений l1 и l2
принимаются равными 1. Аналогично формируется постфиксный образец pa на основе текстовых элементов примера te,
следующих за элементом разметки mr. Образец pc, соответствующий извлекаемой информации, формируется на основе
текстовых элементов, размещенных между элементами разметки ml и mr. Таким образом, все образцы предельно
конкретных правил составляются из элементов ri= < {wj},{},1,1 >, где {wj} - множество из
одного j-ого текстового элемента wj, соответствующего ri - i-ому элементу образца, {} - пустое
множество исключений. Каждое из полученных таким образом правил покрывает ровно один позитивный пример, на основе которого он был получен,
так что на первом этапе обучения имеет место
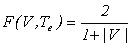
Итеративное обобщение
Итеративное обобщение подразумевает создание новых, более общих правил на основе существующих. Обобщение правил позволяет обученной модели покрывать
большее количество текстовых сегментов предметной области. Процедура итеративна, поскольку на каждом шаге заменяет существующее множество правил
новым множеством только что сформированных обобщенных правил так, что на следующем шаге предпринимаются попытки обобщения новых правил без участия
старых. Алгоритм итеративного обобщения представлен на рис. 3.
V = 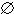 - результирующее множества правил - результирующее множества правил
Vm= исходные предельно конкретные правила
Пока обновляется V
Vk= 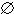 - множества правил, полученных на k-ой итерации - множества правил, полученных на k-ой итерации
G - квадратная матрица обобщений |Vm| X |Vm|
По всем парам (vi,vj) правил из Vm
G[i,j]= обобщение пары правил (vi,vj)
По каждой строке i матрицы M
Если правило vi еще не обработано
C=оптимальный контур, проходящий через vi
По всем ребрам vln контура C
Vk=Vk 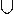 {vln} {vln}
Считать правила vl и vn обработанными все если
Vm =Vk
V=V 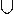 Vk Vk
все пока
Рис. 3. Итеративное обобщение правил.
Итеративное обобщение оперирует с множеством V правил, полученных к текущему шагу и множеством Vm правил, полученных на
текущем шаге. Изначально множество V не содержит ни одного правила, множество Vm содержит предельно конкретные правила,
полученные на первом этапе обучения. Итерации выполняются до тех пор, пока удается пополнить множество V, которое и является результатом
работы алгоритма. На каждой итерации формируется множество Vk обобщенных правил. Для текущего набора правил Vm
формируется матрица обобщения G, каждая ячейка G[i,j] этой матрицы содержит правило vij, полученное в результате
обобщения правил vi Vm и vj Vm и vj
 Vm. Заполненную матрицу G можно рассматривать как ориентированный граф, узлами которого
являются правила из Vm, а любое ребро, исходящее из узла vi в узел vj, взвешено качеством
f(vij) правила vij, полученного при обобщении пары правил (vi,vj). Для каждого узла
графа находится оптимальный контур C, такой, чтобы для каждого узла контура из всех ребер, выходящих из узла, контуру принадлежало бы
ребро с максимальным весом. Обобщенные правила vln, соответствующие ребрам контура C, заносятся в результирующее множество
правил текущей итерации Vk, правила vl и vm, на основе которых образовано vln,
помечаются как обработанные, для исключения их из дальнейшего анализа графа. Оценка качества обобщенных правил f(vij, Te)
выполняется согласно (15). Vm. Заполненную матрицу G можно рассматривать как ориентированный граф, узлами которого
являются правила из Vm, а любое ребро, исходящее из узла vi в узел vj, взвешено качеством
f(vij) правила vij, полученного при обобщении пары правил (vi,vj). Для каждого узла
графа находится оптимальный контур C, такой, чтобы для каждого узла контура из всех ребер, выходящих из узла, контуру принадлежало бы
ребро с максимальным весом. Обобщенные правила vln, соответствующие ребрам контура C, заносятся в результирующее множество
правил текущей итерации Vk, правила vl и vm, на основе которых образовано vln,
помечаются как обработанные, для исключения их из дальнейшего анализа графа. Оценка качества обобщенных правил f(vij, Te)
выполняется согласно (15).
Для сокращения вычислительных затрат при расчете каждой i>f(vij, Te) используется порог
по точности p, задающий минимально допустимую точность обобщенных правил, так что i>f(vij, Te)=0, если.
Такой подход позволяет существенно ограничить число проверок покрытий правилом vij, так если при проверке число покрытий правилом
превысило значение
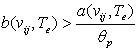 (17) (17)
то правило можно дальше не проверять и принять его качество f(vij,Te)=0. Выигрыш от такого подхода возможен, т.к. для
расчета a(vij,Te) достаточно использовать только часть от всей обучающей выборки Te, состоящую из
позитивных примеров текущего маркера, тогда как расчет b(vij,Te) в общем случае требует определять покрытия по всей Te.
Алгоритм обобщения пары правил
Алгоритм обобщения пары правил (vi,vj) используется при итеративном обобщении (см. рис. 3). Пусть согласно (7) правила
vi и vj представлены в виде троек образцов, т.е. vi=(pbi, pci, pai) и
vj=(pbi, pci, pai). Обобщение выполняется независимо для каждой пары образцов (pbi, pbj), (pci, pcj)
и (pai, paj). Результатом обобщения каждой такой пары являются множества Pb - префиксных обобщенных образцов,
Pc - извлекающих обобщенных образцов и Pa - постфиксных обобщенных образцов. Для каждой тройки (pb, pc, pa)
 Pb X Pc X Pa формируется правило v=(pb, pc, pa),
если v удовлетворяет критерию (17), то выполняется расчет его качества (15). Из всех возможных троек v=(pb, pc, pa)
выбирается единственное правило vij с максимальным качеством f(vij).
При обобщении пары образцов (pi,pj) независимо от их типа (префиксный, постфиксный или извлекающий) выполняются следующие
действия (см. рис. 4). Ключевым элементом алгоритма является матрица соответствий A, в которой строкам соответствуют элементы образца pi, а
столбцам - элементы образца pj. Таким образом, размерность матрицы составляет |pi| X |pj|. Каждая ячейка
матрицы содержит значение Pb X Pc X Pa формируется правило v=(pb, pc, pa),
если v удовлетворяет критерию (17), то выполняется расчет его качества (15). Из всех возможных троек v=(pb, pc, pa)
выбирается единственное правило vij с максимальным качеством f(vij).
При обобщении пары образцов (pi,pj) независимо от их типа (префиксный, постфиксный или извлекающий) выполняются следующие
действия (см. рис. 4). Ключевым элементом алгоритма является матрица соответствий A, в которой строкам соответствуют элементы образца pi, а
столбцам - элементы образца pj. Таким образом, размерность матрицы составляет |pi| X |pj|. Каждая ячейка
матрицы содержит значение 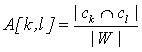 , где ck - лексическое ограничение элемента rk образца
pi, cl - лексическое ограничение элемента rl образца pj, W - множество
всех текстовых элементов естественного языка предметной области. Входной информацией основного алгоритма генерации обобщенных образцов является
пара образцов pi, pj, на основе которых выполняется генерация. Алгоритм заполняет матрицу A соответствия
элементов исходных образцов. Результатом работы алгоритма является множество Pi,j. , где ck - лексическое ограничение элемента rk образца
pi, cl - лексическое ограничение элемента rl образца pj, W - множество
всех текстовых элементов естественного языка предметной области. Входной информацией основного алгоритма генерации обобщенных образцов является
пара образцов pi, pj, на основе которых выполняется генерация. Алгоритм заполняет матрицу A соответствия
элементов исходных образцов. Результатом работы алгоритма является множество Pi,j.
pi , pj - исходные образцы
A-матрица соответствия элементов образцов pi и pj
Pi,j= - итоговое множество образцов - итоговое множество образцов
пополнить Pi,j при pg= , n=0, m=0 - вызов рекурсивного алгоритма (см. ниже)
Рекурсивный алгоритм пополнения множества Pi,j:
Исходные данные рекурсивного алгоритма:
pg текущий формируемый образец
n - текущая строка матрицы A
m - текущий столбец матрицы A
Цикл по k=n+1…|pi|
Цикл по l=m+1…|pj|
если A[k,l]>0, то
r1=новый элемент по правилу (19)
r2=новый элемент по правилу (18)
пополнить Pi,j при pg=pg+r1+r2, n=k, m=l -
(рекурсивный вызов алгоритма)
если Pi,j не пополнилось то Pi,j=Pi,j {pg+r1+r2}
все если
Конец цикла
Конец цикла
Рис. 4. Алгоритмы обобщения пары (pi,pj).
Наполнение множества Pi,j выполняется рекурсивным алгоритмом, приведенным во второй части
рис. 4. Алгоритм просматривает ячейки матрицы, двигаясь по столбцам текущей строки, отыскивая ячейки со
значением A[k,l]>0, обозначающие наличие общности между элементами исходных образцов, соответствующих
номеру строки и столбца. В случае наличия общности генерируются новые элементы по правилам (18) и (19),
обозначения n, m, k и l совпадают с обозначениями в (18) и (19). Правила (18) и (19)
заключаются в следующем:
- Создание нового элемента r на основе пары элементов (rk;rl) таких,
что rk=<ck,ek,l1k,l2k>
является элементом образца pi, а rl=<cl,el,l1k,l2k>
является элементом образца pj. Новый элемент формируется так, что
r=<c,e,l1,l2>, где
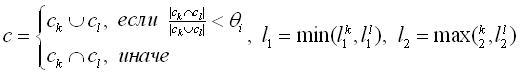 (18) (18)
θi - порог объединения лексических ограничений, определяющий долю совпадающих текстовых
элементов в обоих лексических ограничений, достаточную для взятия их пересечения, вместо объединения
(в экспериментах использовалось значение θi=0,6, определенное опытным путем для
использованной выборки);
- Создание нового элемента r на основе двух пар элементов (rr;rm) и
(rk;rl) исходных образцов pi и pj таких,
что rn и rk являются элементами образца pi
(rn предшествует rk), аналогично rm и rl
являются элементами образца pj (rm предшествует rl).
Новый элемент формируется так, что r=<c,e,l1,l2>, где
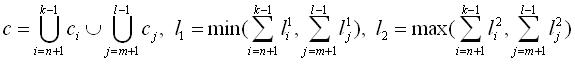 (19) (19)
Назначение правила (18) - создание нового элемента на основе пары лексически близких (похожих) элементов, т.е.
элементов, для которых A[k,l]>0. Назначение правила (19) - формирование нового элемента на основе
"непохожих" элементов исходных образцов, заключенных в промежутке между двумя парами "похожих"
элементов. В алгоритме не отражен тот факт, что правило (19) может генерировать "пустые" элементы,
это возможно, для случая, когда k=n+1 и l=m+1. В таких условиях правило (19) создаст элемент
с пустым лексическим ограничением c=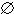 , а значения количеств повторений l1=0 и
l2=0. Такие элементы не добавляются к текущему образцу, т.е. запись
pg=pg+r1+r2, обозначающая присоединение к "хвосту"
образца pg новых элементов r1 и r2, реально вырождается
в запись pg=pg+r2. После "наращивания" pg
начинается рекурсивное выполнение этого же алгоритма, но с новыми начальными условиями, а именно, обновляется
текущий генерируемый образец и увеличиваются нижние границы изменения счетчиков строк и столбцов k и l.
По выходу из рекурсии делается проверка, пополнялось ли множество Pi,j внутри рекурсивного вызова.
Если пополнения не было, то делается вывод, что алгоритм достиг конца одного из образцов, а накопленный к
текущему шагу образец pg+r1+r2 является полностью сформированным очередным
вариантом обобщения, который заносится в Pi,j. Наши эксперименты показали, что критерию
A[k,l]>0 удовлетворяет большинство пар элементов исходных образцов, в результате чего множество
Pi,j содержит чрезмерное количество вариантов обобщения, что в итоге приводит к большому
количеству переборов при оценке троек (pb,pc,pa) , а значения количеств повторений l1=0 и
l2=0. Такие элементы не добавляются к текущему образцу, т.е. запись
pg=pg+r1+r2, обозначающая присоединение к "хвосту"
образца pg новых элементов r1 и r2, реально вырождается
в запись pg=pg+r2. После "наращивания" pg
начинается рекурсивное выполнение этого же алгоритма, но с новыми начальными условиями, а именно, обновляется
текущий генерируемый образец и увеличиваются нижние границы изменения счетчиков строк и столбцов k и l.
По выходу из рекурсии делается проверка, пополнялось ли множество Pi,j внутри рекурсивного вызова.
Если пополнения не было, то делается вывод, что алгоритм достиг конца одного из образцов, а накопленный к
текущему шагу образец pg+r1+r2 является полностью сформированным очередным
вариантом обобщения, который заносится в Pi,j. Наши эксперименты показали, что критерию
A[k,l]>0 удовлетворяет большинство пар элементов исходных образцов, в результате чего множество
Pi,j содержит чрезмерное количество вариантов обобщения, что в итоге приводит к большому
количеству переборов при оценке троек (pb,pc,pa) Pbij X Pcij X Paij. Для сокращения размеров Pi,j
используется следующее ограничение: в Pi,j заносится по одному образцу на каждое
количество L применений правила (18). Из нескольких образцов, полученных одним и тем же количеством L
применений правила (18) выбирается один образец с максимальным весом, рассчитываемым следующим образом
Pbij X Pcij X Paij. Для сокращения размеров Pi,j
используется следующее ограничение: в Pi,j заносится по одному образцу на каждое
количество L применений правила (18). Из нескольких образцов, полученных одним и тем же количеством L
применений правила (18) выбирается один образец с максимальным весом, рассчитываемым следующим образом
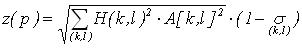 (20) (20)
Где H(k,l)  [0..1] - мера, оценивающая близость позиций k и
l элементов исходных образцов. В нашем случае удобно использовать формулу энтропии [0..1] - мера, оценивающая близость позиций k и
l элементов исходных образцов. В нашем случае удобно использовать формулу энтропии
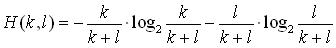 , отражающую степень определенности, с которой можно использовать
rk и rl для генерации элемента по правилу (18) для нового образца.
Чем ближе друг к другу значения k и l, тем ближе H(k,l) к 1, тем с большей
определенностью можно считать rk и rl похожими для применения правила (18).
Значение , отражающую степень определенности, с которой можно использовать
rk и rl для генерации элемента по правилу (18) для нового образца.
Чем ближе друг к другу значения k и l, тем ближе H(k,l) к 1, тем с большей
определенностью можно считать rk и rl похожими для применения правила (18).
Значение 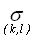 определяет дисперсию нормализованного геометрического расстояния
D(n,m,k,l) между парами элементов исходных образцов, к которым применялось правило (19). D(n,m,k,l)
определяется следующим образом: определяет дисперсию нормализованного геометрического расстояния
D(n,m,k,l) между парами элементов исходных образцов, к которым применялось правило (19). D(n,m,k,l)
определяется следующим образом: 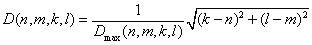 где k, l, n и m -
порядковые номера элементов исходных образцов, для которых применялось (19), Dmax(n,m,k,l)
максимальное геометрическое расстояние для всех пар похожих элементов rk и rl
данного варианта обобщения исходных образцов. Чем меньше дисперсия где k, l, n и m -
порядковые номера элементов исходных образцов, для которых применялось (19), Dmax(n,m,k,l)
максимальное геометрическое расстояние для всех пар похожих элементов rk и rl
данного варианта обобщения исходных образцов. Чем меньше дисперсия 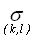 ,
тем более равномерно распределены пары похожих элементов rk и rl в исходных
образцах, тем больше уверенность в пригодности обобщенного образца p. Первая часть выражения (20) (с корнем)
определяет длину вектора размерностью L. Данный вектор ассоциирован с образцом p, координатами
которого являются степени уверенности в выполнении правила (18) для каждой пары похожих элементов rk
и rl исходных образцов из L возможных пар. Таким образом, z(p) учитывает как
лексическую близость A[k,l] элементов исходных образцов, равномерность распределения ,
тем более равномерно распределены пары похожих элементов rk и rl в исходных
образцах, тем больше уверенность в пригодности обобщенного образца p. Первая часть выражения (20) (с корнем)
определяет длину вектора размерностью L. Данный вектор ассоциирован с образцом p, координатами
которого являются степени уверенности в выполнении правила (18) для каждой пары похожих элементов rk
и rl исходных образцов из L возможных пар. Таким образом, z(p) учитывает как
лексическую близость A[k,l] элементов исходных образцов, равномерность распределения 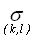 близких элементов по исходным образцам и аналогичность размещения H(k,l) близких элементов в исходных
образцах.
близких элементов по исходным образцам и аналогичность размещения H(k,l) близких элементов в исходных
образцах.
Деградация незадействованных примеров
Деградация незадействованных позитивных примеров выполняется для учета примеров, для которых не было найдено на
этапе итеративного обобщения подходящей пары. Такое возможно, если некоторый обучающий пример описывает уникальное
проявление в тексте извлекаемого значения слота. Такого рода уникальность подразумевает отсутствие аналогов,
поэтому уникальные обучающие примеры не могут образовать пары (vi,vj), заложенные
в основу итеративного обобщения правил. Другой причиной отсутствия аналогов у некоторых примеров является
недостаточная полнота обучающей выборки. В обоих случаях необходимо учесть вклад таких примеров в формирование
модели извлечения. Для этого служит этап деградации незадействованных позитивных примеров.
В данной работе использовалась простейшая стратегия деградации примеров,
когда у каждого примера поочередно удалялся один из текстовых элементов, и на основе полученного "урезанного"
примера формировалось правило аналогично тому, как это выполняется на первом этапе обучения при формировании
предельно конкретных правил из обучающих примеров. Каждое полученное таким образом правило оценивалось
согласно (17), правила проходящие данный критерий подвергались повторной деградации до тех пор, пока
выполнялось (17).
Генерация исключений
Использование критерия (17) допускает генерацию правил извлечения с точностью, находящейся в диапазоне
[θp,1], для повышения качества обученной модели извлечения выполняется генерация
исключений e (см. 4) элементов правил. Для каждого правила вида v=(pb, pc, pa)
формируются исключения только для элементов префиксного и постфиксного образцов, т.е. для pb и
pa. Исключения вводятся следующим образом.
Предположим для определенности, что правило v корректно покрывает
множество Tv текстовых сегментов, в числе которых будут корректные покрытия Tt
(позитивные примеры) и ложные покрытия Tf(негативные примеры), т.е.
Tv=Tt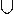 Tf. Из негативных примеров Tf для
каждого элемента ri образцов pb и pa возьмем все
текстовые сегменты Tfi, покрываемые этими элементами. Для устранений ложных покрытий
Tf необходимо сформировать исключение ei лексического ограничения
каждого элемента ri, так что Tf. Из негативных примеров Tf для
каждого элемента ri образцов pb и pa возьмем все
текстовые сегменты Tfi, покрываемые этими элементами. Для устранений ложных покрытий
Tf необходимо сформировать исключение ei лексического ограничения
каждого элемента ri, так что 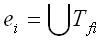 - объединенное множество всех текстовых элементов всех
сегментов, составляющих Tfi. Введя указанным способом исключения, мы явно запретим правилу
покрывать негативные примеры, т.е. обеспечим Tv=Tt. - объединенное множество всех текстовых элементов всех
сегментов, составляющих Tfi. Введя указанным способом исключения, мы явно запретим правилу
покрывать негативные примеры, т.е. обеспечим Tv=Tt.
Результаты экспериментов
Для проверки разработанной модели извлечения и метода ее обучения была создана обучающая выборка, основанная на
стенограммах заседаний Совета Федерации Федерального Собрания РФ. Извлечению подвергались следующие слоты фрейма
"Член Совета Федерации":
- фамилия, члена СФ;
- название комитета, в который входит член СФ;
- название региона, который представляет член СФ.
Количества обучающих примеров для указанных слотов: 603, 234 и 272 соответственно. Оценке подвергалась точность,
полнота и общее качество F(V,Te) обученной модели в зависимости от размера обучающей выборки
и порогового значения p. В экспериментах использовались обучающие выборки размером: 50, 100, 150 и 200
примеров, порог p принимал значения 0.7, 0.8 и 0.9. Каждая обученная модель извлечения тестировалась
на полной обучающей выборки. В таблице 1 приведены оцениваемые показатели в зависимости от указанных входных
параметров. Показатели качества приведены для слотов "Регион" и "Комитет", данные по слоту "Фамилия" не
приводятся, поскольку при подготовке обучающей выборки по данному слоту была допущена ошибка. В строке Err
записаны количества ложных извлечений, выполненных на тестах обученной моделью, в строке Hit - количества
правильных извлечений, Des - количество требуемых извлечений, 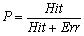 - точность обученной модели, - точность обученной модели,
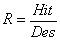 - полнота обученной модели, - полнота обученной модели, 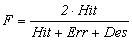 - интегральная
оценка качества обученной модели. Столбцы "шапки" таблицы соответствуют размерам обучающих выборок
50, 100, 150, 200. Вложенные столбцы 0.7, 0.8, 0.9 соответствуют порогам точности θp,
для которых выполнялись обучения. На рис. 5 приведен график зависимости функции качества F обученной модели
извлечения от размера обучающей выборки для слота "Комитет" для θp=0.7. - интегральная
оценка качества обученной модели. Столбцы "шапки" таблицы соответствуют размерам обучающих выборок
50, 100, 150, 200. Вложенные столбцы 0.7, 0.8, 0.9 соответствуют порогам точности θp,
для которых выполнялись обучения. На рис. 5 приведен график зависимости функции качества F обученной модели
извлечения от размера обучающей выборки для слота "Комитет" для θp=0.7.
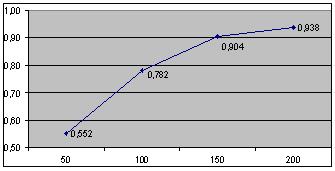
Рис. 5. Зависимость F от размера выборки.
График на рис. 5 позволяет судить об обобщающей способности обучающего метода. Чем больше позитивных примеров
используется для обучения, тем выше качество модели извлечения. Кроме того, график на рис. 5 позволяет судить
о скорости обучения, характеризующей потребный размер обучающей выборки для достижения приемлемого качества.
Обучающий алгоритм аналогичного назначения [4] на 150 примерах достигает F=0.75, в нашем
случае F=0.78
достигается на 100 примерах. Другой алгоритм [2], использующий скрытые Марковские Модели (HMM),
достигает аналогичный показатель качества на 200-300 примерах в зависимости от типа обучающих примеров.
Поскольку в работах [2] и [4] проводились эксперименты над англоязычными
выборками, которыми мы не располагаем, говорить о преимуществах представленного в данной статье метода было бы
не справедливо. Здесь мы всего лишь хотим показать сопоставимость нашего подхода с подходами зарубежных
исследователей.
Заключение
В работе предложена модель извлечения фактов из естественно-языковых текстов предметной области.
В качестве строгого представления фактов используется фреймовая модель, в терминах которой дана постановка задачи
извлечения и описан разработанный метод обучения модели извлечения.
Разработанный метод может быть использован в различных задачах, связанных с
обработкой слабоструктурированных текстов. В частности возможно применение при мониторинге потока новостей для
извлечения конкретных данных по интересующим событиям (место возникновения, участники события и др.).
Табл. 1. Оценка качества обученной модели.
|
50 примеров |
100 примеров |
150 примеров |
200 примеров |
| θp |
0,7 |
0,8 |
0,9 |
0,7 |
0,8 |
0,9 |
0,7 |
0,8 |
0,9 |
0,7 |
0,8 |
0,9 |
| Комитет |
|
| Err |
5 |
5 |
5 |
9 |
8 |
6 |
11 |
10 |
7 |
22 |
14 |
8 |
| Hit |
91 |
89 |
88 |
156 |
145 |
139 |
202 |
190 |
186 |
226 |
226 |
224 |
| Des |
234 |
234 |
234 |
234 |
234 |
234 |
234 |
234 |
234 |
234 |
234 |
234 |
| P |
0,948 |
0,947 |
0,946 |
0,945 |
0,948 |
0,959 |
0,948 |
0,950 |
0,964 |
0,911 |
0,942 |
0,966 |
| R |
0,389 |
0,380 |
0,376 |
0,667 |
0,620 |
0,594 |
0,863 |
0,812 |
0,795 |
0,966 |
0,966 |
0,957 |
| F |
0,552 |
0,543 |
0,538 |
0,782 |
0,749 |
0,734 |
0,904 |
0,876 |
0,871 |
0,938 |
0,954 |
0,961 |
| Регион |
|
| Err |
3 |
3 |
3 |
2 |
3 |
3 |
6 |
5 |
5 |
20 |
11 |
6 |
| Hit |
89 |
89 |
88 |
154 |
153 |
151 |
209 |
191 |
190 |
257 |
250 |
232 |
| Des |
272 |
272 |
272 |
272 |
272 |
272 |
272 |
272 |
272 |
272 |
272 |
272 | s
| P |
0,967 |
0,967 |
0,967 |
0,987 |
0,981 |
0,981 |
0,972 |
0,974 |
0,974 |
0,928 |
0,958 |
0,975 |
| R |
0,372 |
0,372 |
0,324 |
0,566 |
0,563 |
0,555 |
0,768 |
0,702 |
0,699 |
0,945 |
0,919 |
0,853 |
| F |
0,489 |
0,489 |
0,485 |
0,720 |
0,715 |
0,709 |
0,858 |
0,816 |
0,814 |
0,936 |
0,938 |
0,910 |
Другой областью применения данного метода является наполнение онтологий, когда
в качестве источника знаний выступают репрезентативные естественно-языковые тексты предметной области.
В настоящий момент ведется работа по созданию системы выявления несоответствий
между текстами предметной области и ее онтологией. В рамках данной системы разработанный метод используется как
на этапе наполнения онтологии, так и на этапе анализа при извлечении фактов, подвергаемых проверке на предмет
несоответствия.
Литература
The model of fact extraction from natural language texts and the learning method
The model of extracting structured data from natural language texts is proposed. The training method
of such model is also here. The main feature of the model is the extraction rules set. The training method forms
this rules from a human-prepared learning examples. Some experiments are carried out and the main properties of
trained model are shown depends on properties of initial learning examples set.
|
 F имеет набор слотов {sj}. Анализируемый текст t представлен последовательностью элементарных
текстовых элементов {wi}, которыми могут быть слова и знаки препинания. Задача извлечения заключается в формировании
для анализируемого текста набора троек вида <fi,sj,tk>, где fi - фрейм из
предопределенного множества F, sj - слот данного фрейма, tk - фрагмент анализируемого текста t,
являющийся выявленным в тексте t значением слота sj.
F имеет набор слотов {sj}. Анализируемый текст t представлен последовательностью элементарных
текстовых элементов {wi}, которыми могут быть слова и знаки препинания. Задача извлечения заключается в формировании
для анализируемого текста набора троек вида <fi,sj,tk>, где fi - фрейм из
предопределенного множества F, sj - слот данного фрейма, tk - фрагмент анализируемого текста t,
являющийся выявленным в тексте t значением слота sj.

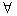 t
t 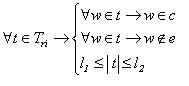 (5)
(5)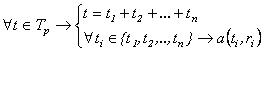 (6)
(6)
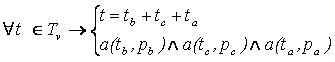 (8)
(8)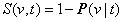 (10)
(10)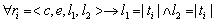 , получив тем самым модифицированное правило v'. Такая замена гарантирует, что v' будет
покрывать только текстовые сегменты, представимые в форме t=t1+t2+...+tn. Таким образом, условную
вероятность P(v|t) можно заменить безусловной P(v'), которая рассчитывается согласно (11)
, получив тем самым модифицированное правило v'. Такая замена гарантирует, что v' будет
покрывать только текстовые сегменты, представимые в форме t=t1+t2+...+tn. Таким образом, условную
вероятность P(v|t) можно заменить безусловной P(v'), которая рассчитывается согласно (11)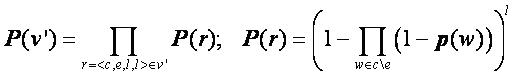 (11)
(11)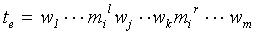 (12)
(12)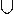 Tm2
Tm2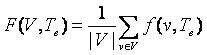 (13)
(13)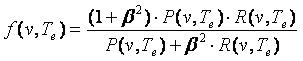 (14)
(14)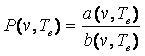 и
и 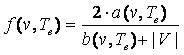 (15)
(15)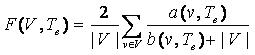 (16)
(16)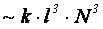 , где l - средняя длина обучающего примера,
N - количество обучающих примеров. Разработанный метод можно разделить на следующие этапы: формирование предельно конкретных правил,
итеративное обобщение, деградация, генерация исключений. Рассмотрим основные этапы метода обучения подробнее.
, где l - средняя длина обучающего примера,
N - количество обучающих примеров. Разработанный метод можно разделить на следующие этапы: формирование предельно конкретных правил,
итеративное обобщение, деградация, генерация исключений. Рассмотрим основные этапы метода обучения подробнее.
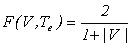
 - результирующее множества правил
- результирующее множества правил
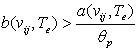 (17)
(17)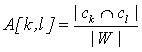 , где ck - лексическое ограничение элемента rk образца
pi, cl - лексическое ограничение элемента rl образца pj, W - множество
всех текстовых элементов естественного языка предметной области. Входной информацией основного алгоритма генерации обобщенных образцов является
пара образцов pi, pj, на основе которых выполняется генерация. Алгоритм заполняет матрицу A соответствия
элементов исходных образцов. Результатом работы алгоритма является множество Pi,j.
, где ck - лексическое ограничение элемента rk образца
pi, cl - лексическое ограничение элемента rl образца pj, W - множество
всех текстовых элементов естественного языка предметной области. Входной информацией основного алгоритма генерации обобщенных образцов является
пара образцов pi, pj, на основе которых выполняется генерация. Алгоритм заполняет матрицу A соответствия
элементов исходных образцов. Результатом работы алгоритма является множество Pi,j.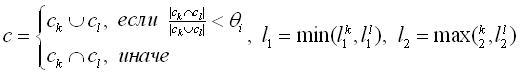 (18)
(18)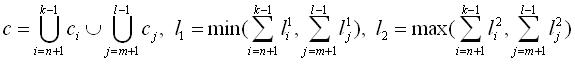 (19)
(19)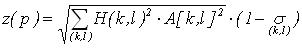 (20)
(20)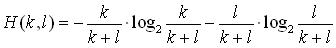 , отражающую степень определенности, с которой можно использовать
rk и rl для генерации элемента по правилу (18) для нового образца.
Чем ближе друг к другу значения k и l, тем ближе H(k,l) к 1, тем с большей
определенностью можно считать rk и rl похожими для применения правила (18).
Значение
, отражающую степень определенности, с которой можно использовать
rk и rl для генерации элемента по правилу (18) для нового образца.
Чем ближе друг к другу значения k и l, тем ближе H(k,l) к 1, тем с большей
определенностью можно считать rk и rl похожими для применения правила (18).
Значение 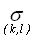 определяет дисперсию нормализованного геометрического расстояния
D(n,m,k,l) между парами элементов исходных образцов, к которым применялось правило (19). D(n,m,k,l)
определяется следующим образом:
определяет дисперсию нормализованного геометрического расстояния
D(n,m,k,l) между парами элементов исходных образцов, к которым применялось правило (19). D(n,m,k,l)
определяется следующим образом: 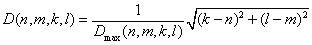 где k, l, n и m -
порядковые номера элементов исходных образцов, для которых применялось (19), Dmax(n,m,k,l)
максимальное геометрическое расстояние для всех пар похожих элементов rk и rl
данного варианта обобщения исходных образцов. Чем меньше дисперсия
где k, l, n и m -
порядковые номера элементов исходных образцов, для которых применялось (19), Dmax(n,m,k,l)
максимальное геометрическое расстояние для всех пар похожих элементов rk и rl
данного варианта обобщения исходных образцов. Чем меньше дисперсия 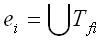 - объединенное множество всех текстовых элементов всех
сегментов, составляющих Tfi. Введя указанным способом исключения, мы явно запретим правилу
покрывать негативные примеры, т.е. обеспечим Tv=Tt.
- объединенное множество всех текстовых элементов всех
сегментов, составляющих Tfi. Введя указанным способом исключения, мы явно запретим правилу
покрывать негативные примеры, т.е. обеспечим Tv=Tt.
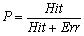 - точность обученной модели,
- точность обученной модели,
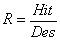 - полнота обученной модели,
- полнота обученной модели, 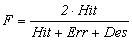 - интегральная
оценка качества обученной модели. Столбцы "шапки" таблицы соответствуют размерам обучающих выборок
50, 100, 150, 200. Вложенные столбцы 0.7, 0.8, 0.9 соответствуют порогам точности θp,
для которых выполнялись обучения. На рис. 5 приведен график зависимости функции качества F обученной модели
извлечения от размера обучающей выборки для слота "Комитет" для θp=0.7.
- интегральная
оценка качества обученной модели. Столбцы "шапки" таблицы соответствуют размерам обучающих выборок
50, 100, 150, 200. Вложенные столбцы 0.7, 0.8, 0.9 соответствуют порогам точности θp,
для которых выполнялись обучения. На рис. 5 приведен график зависимости функции качества F обученной модели
извлечения от размера обучающей выборки для слота "Комитет" для θp=0.7.
